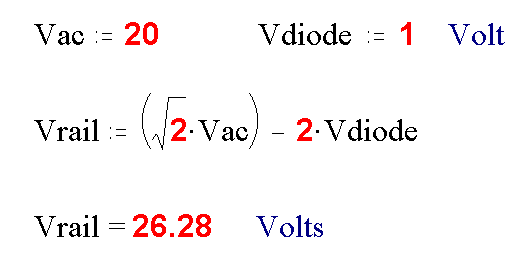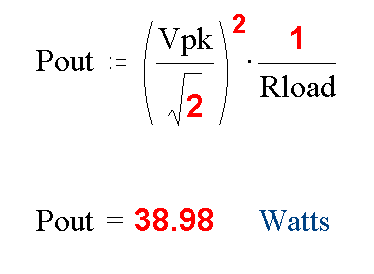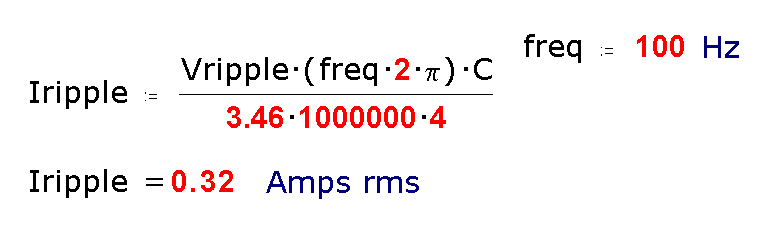The Signal Transfer Company: Power Output

Application Note 1. Power Output Calculations.

This page gives information on calculating transformer and power supply requirements for an audio power amplifier. No serious mathematics is required- nothing beyond square roots. These calculations assume a simple unregulated power supply consisting of a mains transformer, bridge rectifier, and reservoir capacitors. This may appear unsophisticated, but in fact is appropriate for even the very highest quality requirements.
The power amplifier PCBs we sell are capable of giving a wide range of power outputs, up to a maximum that is set by the number of output devices fitted and the size of heatsink they are fixed to.
The upper limits of the power available from a Signal Transfer PCB are set not so much by the components on the PCB as by its basic topology. For example, the MPSA42/92 small-signal transistors used have a 300V rating, but that certainly does not mean you can use +/-150V supply rails and drive a kilowatt into 8 Ohms. As the power output demanded increases, the current that must be provided by the driver transistors also increases, until they are unable to provide it, either because their ratings are exceeded or because the resulting non-linearity becomes unacceptable. At high power levels, usually well above those used in domestic hifi, it is necessary to use a pre-driver stage to get sufficient current gain.
You probably have some idea of what power you want from your amplifier project; alternatively you may have a likely-looking transformer to hand and you would like to know what power it would give you, and if it has enough current capability. Transformers are not cheap, and there is always a strong incentive to use what you have.
It might as well be said at once that this calculation is not going to be super-accurate. This is because in any rectified supply current is not drawn from the transformer continuously, as would happen if a resistor was connected across the secondary, but in relatively short pulses of high current that charge up the reservoir capacitors. Current can neither be created or destroyed in a circuit, and the current coming out is fixed by what we need, so it is clear that the shorter the charging pulses, the larger they must be.
The length of these pulses is usually about 3 msec, while the time for half a cycle is 10 msec- in Europe, anyway, where the mains supply is at 50Hz. Therefore the power supply reservoir capacitors charge for 3 msec and discharge for 7 msec. This latter figure is also important, and we will use it later.
However, the exact length, waveshape and peak value of these charging pulses is not well defined and not easy to predict. It depends on transformer winding resistances and leakage inductances- the latter in particular are not easy to deal with. It is most unlikely you will find a transformer manufacturer who is prepared to design to a specified value of leakage reactance.
The narrower the pulses and the higher their peak current value, the greater losses the losses in the transformer winding resistance, the less voltage you will get out, and the greater the transformer I-squared-R heating.

THE DESIGN CALCULATIONS.

1) DETERMINE DC RAIL VOLTAGE.
Assuming the usual bridge rectifier, simply multiply the transformer nominal rms voltage by the square root of two, to get the peak voltage, and then subtract a couple of volts to allow for rectifier losses.
(Two or more volts may seem like a lot to subtract, but remember that in bridge rectification there are always two diodes conducting between transformer and reservoir capacitor. This sounds like it might be a loss of 0.6V x 2, but in fact the diode drop is much greater than the "standard" 0.6V because of the high peak currents)

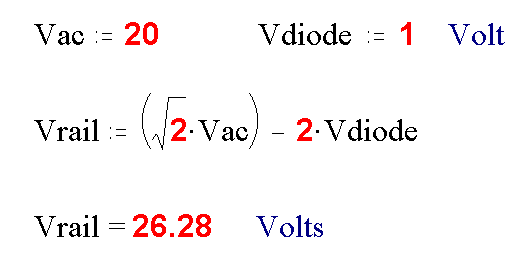
Now you have calculated Vrail, you can choose the voltage rating of the bridge rectifier and the reservoir caps.

2) DETERMINE MAX OUTPUT VOLTAGE SWING.
This is a bit more complicated. Practical amplifiers are not 100% voltage-efficient; in other words, if your amplifier is powered from +/-40V rails, you're not going to get an output swing of 80V peak-to-peak, even without a load. The internal nodes of the amplifier cannot get right to the rails, because of voltage drops across saturated transistors & so on.
There is also another way in which output swing is lost; all amplifiers have some output resistance. Ignoring the effects of feedback, most of this is in the form of the output device emitter resistors, which form a potential divider with the output load. You must now decide the load impedance you're aiming for. Once again, that's a lot more complex than it sounds. Load impedances are almost always specified as pure resistances, while real loudspeakers look nothing like a pure resistor. The impedance curve usually looks like a mountain range.

Here the first step is to subtract the Vsat from Vrail. The effect of the Re-Rload potential divider is then calculated, giving the peak output voltage Vpk. Note this is half of the total output swing, since we began with one rail voltage.

3) DETERMINE POWER OUTPUT.
Take the max peak output voltage and divide by the square root of two, to get the max rms output voltage. This is then squared and divided by the load resistance to give power out.

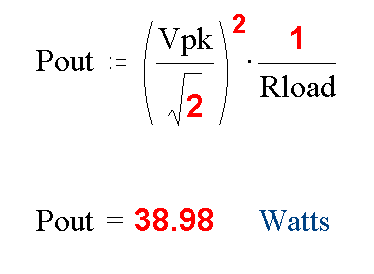
You will note the sweeping assumptions made here. The square-root-of-two factor assumes the waveform is sinusoidal, which it is not.
The load is assumed to be a pure resistance, which it is not.
This may lead you to suppose that these calculations are pretty pointless- but then consider the alternative. Every piece of music has its own "waveform", and every speaker its own complicated impedance curve; each combination would give different results. In fact the sinewave case is more demanding than music in terms of heating and output device stress; in contrast a resistive load is always kinder to the output transistors than a reactive load.

4) DETERMINE PEAK OUTPUT CURRENT AND AVERAGE SUPPLY CURRENT.
You need to know the peak current to make sure it is within the capabilities of the output devices, which means less than Ic(max) on the data sheet. Having obtained Ipk simply by using Ohm's Law, it is also used to calculate Iavg, the average current drawn from the supply. The critical factor here is the Pi in the second equation, which converts the peak value of a half-wave rectified sinewave (remember that each rail only provides power on one half of the cycle) to the equivalent continuous current.

Now you have Iavg, you can select the current ratings of the mains transformer and the bridge rectifier. You can also check the power rating of the emitter resistors.

5) DETERMINE RAIL RIPPLE VOLTAGE.
You need to know this for two reasons; firstly to make sure that the ripple is not large enough to seriously reduce the output voltage capability. The output will clip first on the bottom of the ripple troughs, and these get deeper as the ripple voltage increases; the peak value is pretty much constant, being set by the transformer secondary voltage.
Excessive rail ripple will of course also be harder to keep out of the circuitry, possibly leading to audible hum in some designs- though not those we sell, which have unusually good power-supply rejection...
The other reason is that the ripple voltage sets the amount of ripple current flowing through the reservoir caps.

Here we use the fact that the capacitor discharge time Tdisch is approx 7 msec. The factor of 1000 on the bottom of the equation is just scaling so that C can be conveniently entered in microfarads.

6) DETERMINE RESERVOIR RIPPLE CURRENT.
The reservoirs are capacitors, they have an AC voltage across them, and so AC current flows through them; this causes heating, and if excessive will destroy the capacitor. Even modest heating will reduce capacitor life. The ripple current rating is in the capacitor manufacturer's spec.

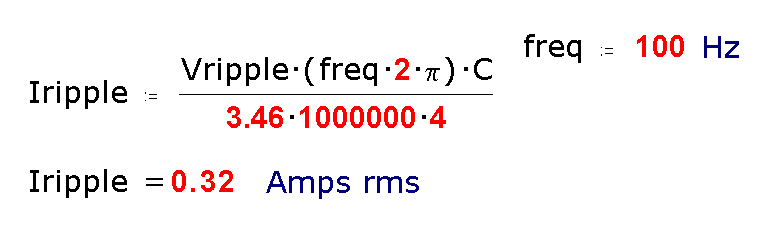
This equation is a little more obscure than the previous ones. The 2Pi factor converts freq to angular frequency, and the factors on the bottom set the scaling so C is in microfarads, and allow for the non-sinusoidal ripple waveform.
If Vripple and hence Iripple is too great, typically you will have to use more capacitors. Simply doubling the capacitance in the same can will probably gain you nothing, as the ripple voltage will be halved,the but the capacitance is doubled, so the same amount of ripple current will be flowing. The answer is to use two capacitors in parallel rather than one; the ripple current is now split between two components. Each capacitor therefore now experiences half of the original ripple current heating.

The Signal Transfer Company accepts no liability for any loss or damage consequent to the use of the information given here.